Third Term Social Studies Lesson Note for JSS2

ACCESS ALL LESSON NOTES

ACCESS ALL QUESTIONS AND ANSWERS

ACCESS ALL WORKSHEETS

ACCESS ALL JOBS ACCESS

ACCESS WAEC QUESTIONS AND ANSWERS

ANGLES IN A POLYGON

CONTENT

1. Definition of Polygons
2. Types Of Polygons
3. Sum of Interior Angles in a Polygon
4. Sum of Exterior Angles in a Polygon

 

Definition of Polygons

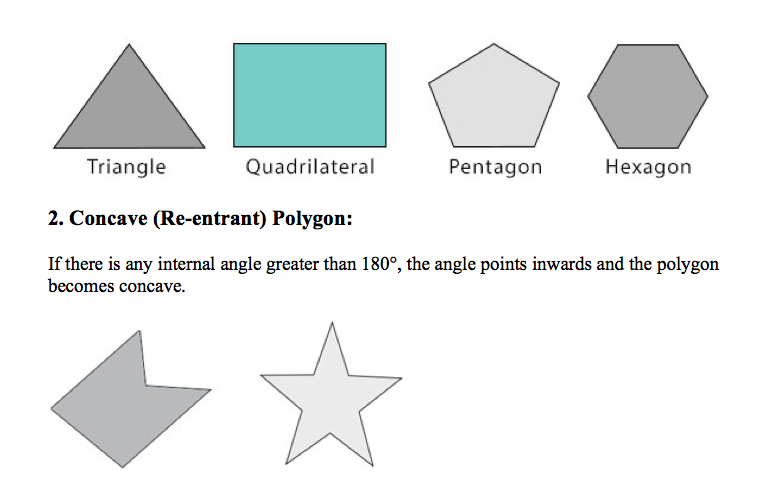
A closed plane figure bounded by straight lines (edges) is called a polygon. The number of sides of a polygon determines its names. The table below describes the names of polygons according to the number of their sides:

	No. of sides and angles	Polygon
	3	Triangle
	4	Quadrilateral
	5	Pentagon
	6	Hexagon
	7	Heptagon
	8	Octagon
	9	Nonagon
	10	Decagon
	11	Undecagon/Hendecagon
	12	Dodecagon
	15	Pentadecagon
	20	Icosagon

 

Types Of Polygons

1. Convex Polygon:

A convex polygon has all its interior angles pointing outwards. No angle is pointing inwards. Each internal angle of a convex polygon is always less than 180⁰. A polygon is convex if any line segment joining any two points on it stays inside the polygon itself. Examples of convex polygons are shown below:

3. Regular Polygon:

This is a polygon with all its angles the same size and all its sides the same length.

4. Irregular Polygon:

This is a polygon with at least two of its sides of different length and at least two of its angles unequal.

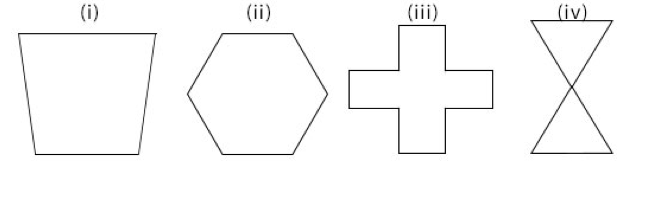
CLASS ACTIVITY

For each of the polygons drawn below, state (i) whether it is concave or convex (ii) whether it is regular or irregular (iii) its name according to the number of sides.

Sum of Interior Angles in a Polygon

The sum of interior angles in a polygon is derived from the number of triangle that can be drawn from the polygon. Consider the diagrams below:

From the above diagrams;

4 sided Quadrilateral has 2 triangles, 5 sided Pentagon has 3 triangles and 6 sided hexagon has 4 triangles. We can therefore say that a n-sided polygon has n – 2 triangles.

Since sum of angles in a triangle is 180^o;

A polygon with 4 sides having 2 triangles will have 2 × 180^o= 360^o

A 5-sided polygon having 3 triangles will have 3 × 180^o = 540^o

A 6-sided polygon having 4 triangles will have 4 × 180^o = 720^o

In general, the sum of the interior angles of any convex n-gon (polygon with n sides) is given by:

Sum of interior angles = (n − 2) × 180⁰ = (n − 2) × 2 × 90

Or Sum of interior angles = (2n − 4) × 90⁰

Or Sum of interior angles = (2n – 4) Right angles

For a regular polygon that has all its sides and angles equal, the size of each interior angle will be the average of the sum of all interior angles

Therefore each interior angle for a regular convex polygon

Each interior angle = sum of interior anglesnumber of sides

= n−2×180on

Example 1:

What is the sum of the interior angles of a pentagon?

Solution:

A pentagon has five sides, that is, n = 5.

Therefore, sum of interior angles = (n − 2) × 180⁰

= (5 − 2) × 180⁰

= 3 × 180⁰ = 540⁰

Example 2:

Calculate the size of each interior angle of a regular heptagon.

Solution:

A regular heptagon has 7 equal sides, that is, n = 7.

Each interior angle = sum of interior anglesnumber of sides

= n−2×180on

= 7−2×180o7 = 5×180o7

= 900o7

= 12857o

CLASS ACTIVITY

1. What is the sum of interior angles of a: (a) hexagon (b) nonagon
2. The sum of six of the interior angles of a nonagon is 920⁰. The other three angles are all equal. Find the size of each of the other three angles.
3. If the angles of a quadrilateral are x, 2x and 3x, what is the value of x? Calculate the size of the largest angle.

 

Sum of Exterior Angles in a Polygon

Sum of exterior angles in any polygon = 360⁰

Example 1:

The sum of the interior angles of a regular polygon is 10 right angles.

(i) How many sides has the polygon?

(ii) What is the sum of the exterior angles of the polygon?

(iii) Calculate the size of each exterior angle of the polygon.

Solution:

Sum of interior angles = (n − 2) × 180⁰

= (n − 2) × 2 × 90⁰

Sum of interior angles = (2n − 4) × 90⁰

Sum of interior angles = (2n − 4) right angles

2n – 4 = 10

2n = 10 + 4

2n = 14

Therefore, n = 7 sides

(i) Sum of exterior angles = 360⁰

(ii) Each exterior angle = sum of exterior anglesnumber of sides

= 360o7

= 5137o

CLASS ACTIVITY

1. Calculate the size of each exterior angle in a regular: (a) octagon (b) decagon
2. Is the sum of exterior angles of a triangle equal to the sum of exterior angles of an Icosagon?

ANGLES OF ELEVATION AND DEPRESSION

CONTENT

1. Horizontal and Vertical Planes
2. Angles of Elevation and Depression
3. Measuring Angles of Elevation and Depression
4. The Relationship between Angle of Elevation and Depression
5. Scale Drawing

 

Horizontal and Vertical Planes

An horizontal plane lies (flat) in the same position as the ground while a vertical plane stands like a straight wall.

 

Angles of Elevation and Depression

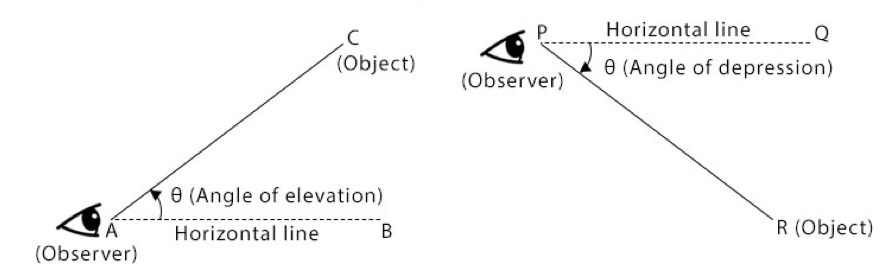
Angle of Elevation

The angle that an observer would raise his or her line of sight above a horizontal line in order to see an object. The angle of elevation is the angle between the horizontal and the observer’s line of sight.

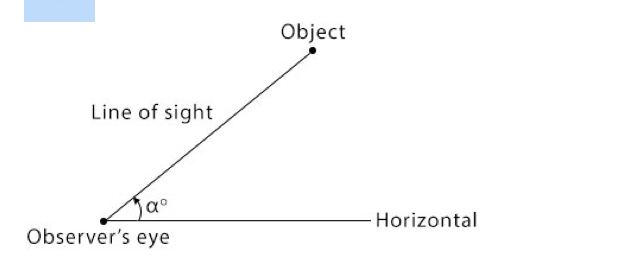
In the diagram above, the angle of elevation of the object from the observer is α⁰.

Angle of Depression

If the object is below the level of the observer, then the angle between the horizontal and the observer’s line of sight is called the angle of depression. If an observer wereup above and needed to look down, the angle of depression would be the angle that the person would need to lower his or her line of sight.

Measuring Angles of Elevation and Depression

Angles of elevation and depression can be measured with a simple instrument called Clinometers. Simple Clinometers is made from a chalk-board protractor in which a plumb-line hangs from the center of the protractor. The angle that the plumb-line makes with the 90⁰ vertical axes when the Clinometers is placed in the observer’s direction is the angle of elevation or depression.

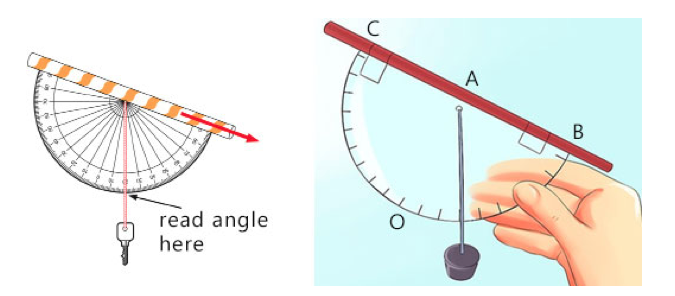
In the figure above, a plumb-line hangs from the center of the protractor at A. The observer sights an object along the line BAC. The angle of elevation e⁰ is the angle between AO and the plumb-line. The size of e⁰ can be read from the scale. Notice that e⁰ increases from 0⁰ at O to 90⁰ at B.

NOTE: The teacher should make simple clinometers using a chalk-board protractor and plumb-line.

CLASS ACTIVITY

Carry out the following activities using a tape and clinometers:

1. Stand at a point Y on level ground, where the top of the wall in your class has an angle of elevation of 45⁰
2. Find the distance from Y to the base of the wall in your class. Record the height of the wall.

 

The Relationship between Angle of Elevation and Depression

In other words, as shown in the diagrams below, the angle formed with the horizontal when an observer looks up is called angle of elevation whereas, the angle formed with the horizontal when an observer looks down is called angle of depression.

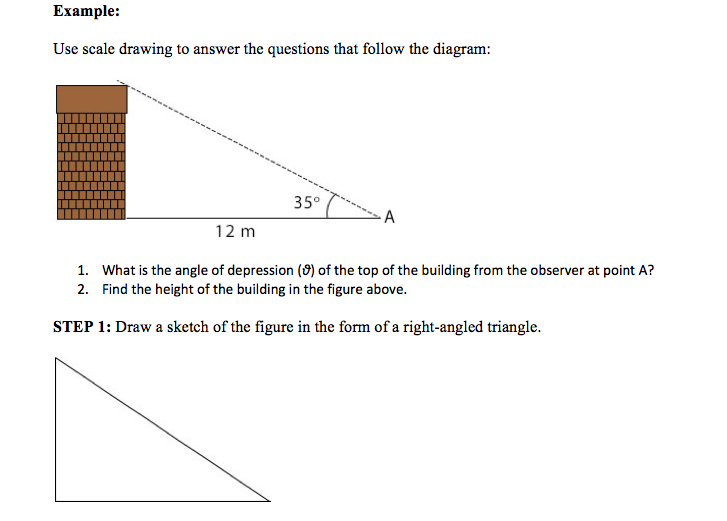
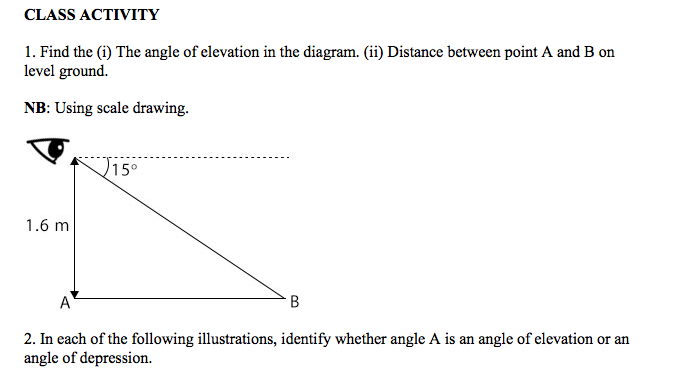
3. When the elevation of the sun is 33^o, a student has a shadow of 2.9m long. Make a scale drawing and find the height of the student to the nearest 5cm.

PRACTICE QUESTIONS

1. (a) What is the angle between the minute-hand and hour-hand of a clock at 3 0’clock.

(b) Find the angle between the hands of a clock at 7 0’clock.

2. From the top of a tower 14 m high, the angle of depression of a student is 32^o. Make a scale drawing and find the distance of the student from the foot of the tower to the nearest ½ m.

BEARING AND DISTANCES

CONTENT

1. The Compass Directions
2. Major Compass/Cardinal Directions
3. Minor Cardinal Directions
4. Bearing and its Types
5. The Compass and Compass/Directional Bearing
6. The Acute Angle or Simple Bearing
7. The Three-figure or Surveyor’s Bearing
8. Directional versus Three-figure versus Acute Angle Bearing
9. Reciprocal/Back Bearing
10. Scale Drawing

 

 

The Compass Directions

Major Compass/Cardinal Directions

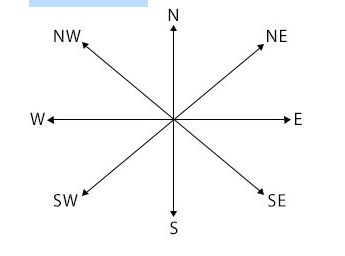
There are four major directions used to describe locations. These cardinal directions are:

North (N)    South (S)    East (E)    West (W)

The four main directions, North, South, East and West, divide the angle at a point (360^o), into four equal parts and each is 90^o or a right angle.

Minor Cardinal Directions

Other minor cardinal directions are those that lie in the midpoints as follows:

North and East called North-East (NE)

South and East called South-East (SE)

South and West called South-West (SW)

North and West called North-West (NW)

These minor cardinal directions subdivide each right angle into two equal parts such that the angle between each major cardinal and minor direction is 45^o. The eight cardinal points are illustrated below:

TO GET YOUR COMPLETE LESSON NOTE AT AN AFFORDABLE PRICE, HIT THE WHATSAPP BUTTON BELOW

VIEW ALL SCHEME OF WORK

ACCESS ALL LESSON NOTES

ACCESS ALL QUESTIONS AND ANSWERS

ACCESS ALL WORKSHEETS

ACCESS ALL JOBS ACCESS

ACCESS WAEC QUESTIONS AND ANSWERS